Sorting is one of the fundamental operations in computer science which is used for many real-time applications managing large data sets. Sorting generally refers to arrangement of data in a certain order. Merge sort is one of the popular and efficient sorting method. This will break larger problem into pieces, sort them and combine them back together.
Here, we will learn the general principle of merge sort and afterwards we will see an example and implementation of this algorithm in Python.
What is Merge Sort?
Merge sort is a divide-and-conquer algorithm. This generally means that the problem is divided into multiple sub-problems, which are then divided by the same algorithm into more sub-problems. This procedure goes on until the sub-problems become very easy to solve.
When we reach this point, the sub-problems are then combined to solve the original problem. This will probably make a lot more sense, when we work through the example of Merge sort.
Merge sort algorithm has o(n*log(n)) running time, which is the optimal running time for comparison-based algorithms.
Suppose we want to sort an array using merge sort:
- The general principle is to split this array in half.
- Afterwards call merge sort on each half to sort those halves recursively.
- Third step is to merge both sorted halves into one sorted array.
So, here you can find this divide and conquer principal that just divides the problem of sorting a whole array into sorting two array of half the size. This will continue until we have just array of size one to sort. This problem will be very easy because array of size one is always sorted
To explain this further, we will see an example and this should clarify all the details of merge sort.
For example:
Let us sort an array of seven numbers[2,6,5,1,7,4,3] using Merge sort.

1. First of all, we start with the dividing step of merge sort. Therefore, this array is split into two parts and we will look for the middle point.

i. In this case we have seven numbers, one side will be slightly bigger than the other but there is no problem. We just split and save the two sub-arrays into two new arrays.
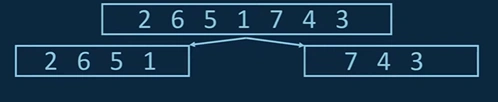
This division goes on recursively.
ii. We first look at the left part and divide it even further.

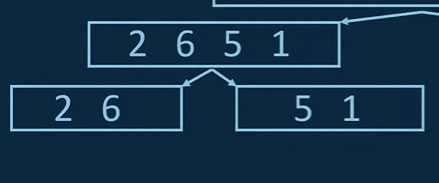
iii. We look at the right sub-array and divide this array even further and this dividing step will go on until all of the sub-arrays have just one entry left.
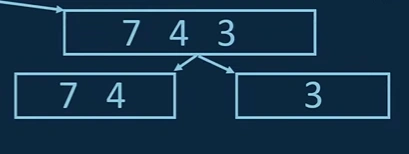
iv. When we have one entry left, the array will be already sorted and then only we can start with combining.

2. We can now start with the merging step that is to merge the smaller arrays into slightly bigger array that are already sorted.
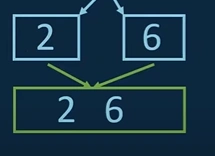
i. Therefore, we start with the 2 and 6 and want to bring 2 & 6 into the right order.
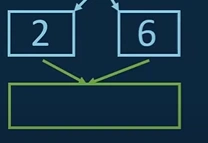
ii. Therefore, we compare 2 and 6 and see that 2 is less than 6. First save 2 in the new array and afterwards save 6 into this new array.
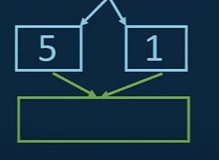
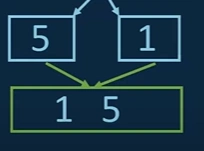
iii. The same procedure will be applied to 5 and 1. We will compare 5 and 1. Obviously, 1 is less than 5 and will save 1 into the new array and afterwards 5.
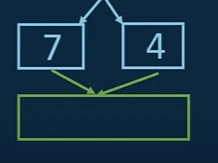
iv. Again, the same applies to the 7 and 4. We will save 4 first and then 7.
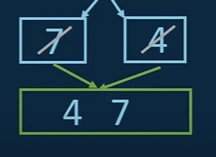
v. 3 is left untouched for now and further we will build arrays of size 4 that are already sorted.
vi. In this step, we want to bring [2,6,1,5] into the right order.
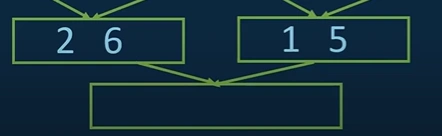
We just need to compare the leftmost elements of both the arrays.
vii. Firstly, we will compare 1 & 2, we see that, 1 is less than 2. We will save 1 first into the array.
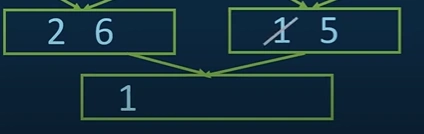
Afterwards, we will compare 2 and 5. As five is now the leftmost element in the right array.
viii. We see that 2 is less than 5 and will save 2 into the new array.
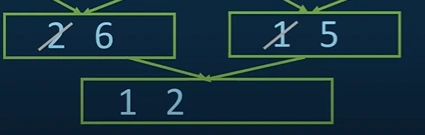
ix. We just need to compare 6 and 5 and will push the smaller one in the array first.
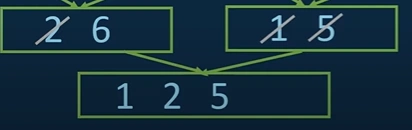
x. There is nothing to compare with six. So, it will directly transfer into the new array.
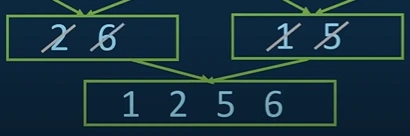
xi. Next, we will build a bigger array out of [4,7,3] by applying the same procedure.
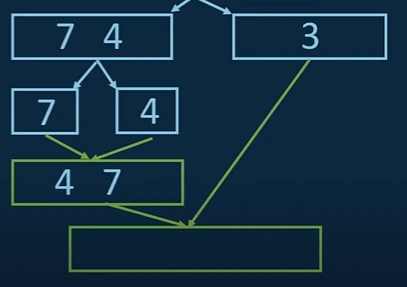
We compare 3 and 4, because they are the leftmost elements of the two arrays.
3 is less than 4 and here we just have to save 3 in the new array and cross it out.
xii. Now, there’s nothing left to compare 4 and 7 to and they are already in the right order. We can just transfer them into the array directly.
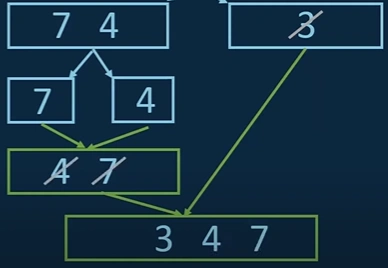
3. Going forward towards last merging step, this will finish our merge sort algorithm.

i. In this case, we just start by comparing 1 and 3 because one and three are the leftmost elements.
ii. Storing 1 in the new array first, as it is smaller than 3.

iii. Next, we could pair two and three. Storing two in the array.
iv. Compare five and three, Store three in the array.
v. Compare five and four, store 4 in the array.
vi. Compare five and seven, store 5 in the array.
vii. Compare six and seven, store 6 in the array.
viii. This all just leaves us with 7 only. 7 will be directly transferred to the array.

This just shows the divide-and-conquer principle where we divided the array until we are left with a simple problem of array of size 1.
In sorting and the merging step, we just combined very small and easy to solve arrays to big array, until we got our initial array in sorted order.
Hopefully, this example helped you to understand the algorithm and now we will see the implementation part of data structure algorithm.
Also check the tree data structure implementation in python
Implementation of merge sort algorithm
Let us define an example array that will give us something to test our implementation on.
def merge_sort(arr): - For the implementation, we define a function called merge sort. In Python, you define a function using ‘def’ keyword and then write the function name and arguments in parentheses.
- In this case we only have one argument i.e. an array.
- This function only works, if the length of the array which we have choose to sort is greater than 1. If the array length is not greater than 1, it shows that the array is already sorted and we have nothing to do with it.
Defining the recursion part of this algorithm
merge_sort(left_arr)
merge_sort(right_arr) - We need to define two sub arrays, one that goes from the beginning to the middle point of an original array and one goes from the middle point to the end of that array.
- In Python you have this special notation to get slices of an array.
left_arr = arr[:len(arr)//2]
right_arr = arr[len(arr)//2:] - This returns a slice of the original array(left array) beginning at index 0 at ending at the index (length of array/2).
- The right array on the other hand starts at (length of array/2) and goes up to the end.
- If you leave a ‘blank space’ before colon, this automatically means a 0 and if you leave a ‘blank’ after the colon, this has the same meaning as if you would insert (length of array).
- Double slash(//) here represents that you want to do integer division. In simple words, you would get a decimal out of this computation but it will be rounded off to the next integer.
Calling merge sort function
Logic:
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] < right_arr[j]:
arr[k] = left_arr[i]
i += 1
else:
arr[k] = right_arr[j]
j += 1
k += 1
while i < len(left_arr):
arr[k] = left_arr[i]
i += 1
k += 1
while j < len(right_arr):
arr[k] = right_arr[j]
j += 1
k += 1- This just means that, we will perform the merge sort algorithm on both the left and right array.
- After this, we will get both the arrays in sorted order.
- Remember, after getting two portions in sorted form, we will begin to merge them and make a bigger array out of them in sorted form.
- We will compare the left most element of left array to the leftmost element of the right array.
- We will use index ‘i’ to keep track of the leftmost element in left array and index ‘j’ to keep track of the leftmost element in right array.
- Next, we will use while loop and inside this loop, we will do comparison between the left array at index ‘i’ with the right array at index ‘j’.
- A new variable k will be defined which will keeps track of the indexes in the new(merged) array.
- Now, when we see that the left array is smaller than right array at current indexes: We can save the value of our left array inside of merged array. Then we just have to increment ‘i’ and ‘k’.
- When right array is smaller than the left array at current indexes or they are equal: In this case, we will save the right array index j in the merged array. We have to increment j and k.
- Now imagine, we already looked at every element in the right array and have already copied all elements from the right array to the merged array: We will simply copy the remaining elements from the left array to the merged array. This happens only when ‘i’ is still smaller than the length of the left array. Afterwards, we need to increase both indexes i.e. ‘i’ and ‘k’.
- We need to implement this case, that every element from the left array is already in sorted array but there are some missing elements of the right array: We just do very similar thing as we did in case of left array. But in this case, firstly we check if we are not at the end of the right array. Then, we just assign every element of the right array to our merged array.
- Now, we can just go down to our test array and call our merge sort function to see if we were successful with our implementation.
- We will run the code.
- You will see a perfectly ordered array on your console screen which shows that you are successful done with merge sort algorithm.
Implementation of Merge Sort in Python:
def merge_sort(arr):
if len(arr) > 1:
left_arr = arr[:len(arr)//2]
right_arr = arr[len(arr)//2:]
# recursion
merge_sort(left_arr)
merge_sort(right_arr)
# merge
i = 0 # left_arr index
j = 0 # right_arr index
k = 0 # merged array index
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] < right_arr[j]:
arr[k] = left_arr[i]
i += 1
else:
arr[k] = right_arr[j]
j += 1
k += 1
while i < len(left_arr):
arr[k] = left_arr[i]
i += 1
k += 1
while j < len(right_arr):
arr[k] = right_arr[j]
j += 1
k += 1So far, we have explored the working and implementation of Merge-sort algorithm. This might seem difficult at the first sight due to the concepts used but once we practice by ourself, it becomes very hands-on. It has been a reliable algorithm especially while working with large datasets.
Learn more about data structure algorithms in our Python advance course in Delhi or python online course
Keep Practicing and Learning.

